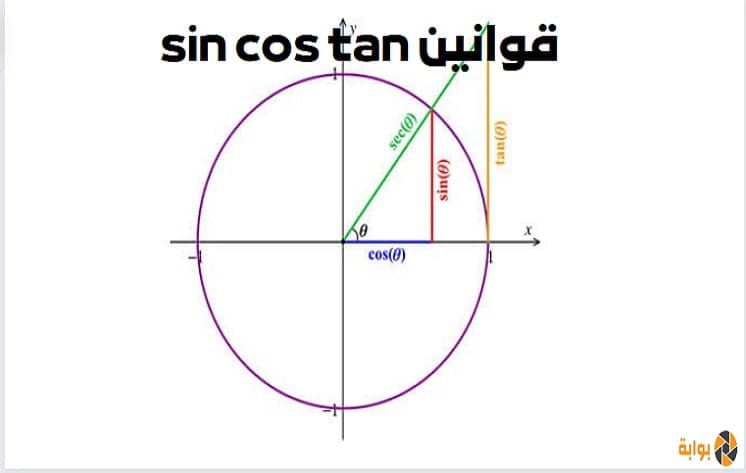
ما هي قوانين sin cos tan الزوايا المثلثية
نتقدم إليكم بمجموعة قوانين sin cos tan وهي من الزوايا المثلثية الشهيرة في علم الرياضيات، فالمثلث هو من الأشكال الهندسية المغلقة والأكثر بروزًا في العلم، ويتكون من ثلاث زوايا وهناك ثلاثة أنواع منه كما نعرف، وكل زاوية من تلك الزوايا المذكورة لها علاقة مع الأخرى، وكل ذلك سنتعرف عليه معًا من خلال السطور القادمة لموضوع اليوم.
قوانين sin cos tan الزوايا المثلثية
بالنسبة إلى قوانين sin cos tan فإن لكل زاوية قانون نحتسب منه الزاوية المطلوبة، فإن قيمتها هامة في قسم حساب المثلثات، ونستخدم النسب بينهم في دراسة العلاقات المختلفة بين الزوايا خاصة في المثلث قائم الزاوية، وأول العلماء الذين أنشؤوها هو العالم الرياضي الشهير فيثاغورث، من خلال دراسته العلاقة بين أضلاع المثلث عبر نظريته الشهيرة، وربط الأضلاع بزوايا مثلثية من خلالها.
إن أطول ضلع من أضلاع المثلث في النوع القائم الزاوية يُعرف باسم “الوتر”، وضلعيه الآخرين هما المقابل والمجاور، وبمعرفة الثلاثة أضلاع يمكننا أن نحتسب قيم الزوايا المثلثية (جا – جتا – ظا) أو (sin – cos – tan)، فالضلع المقابل هو الذي يُقابل الزاوية المعينة، بينما المجاور فهو الملامس للزاوية نفسها ويلامسها الوتر من الجانب الآخر.
حيث أن قوانين sin cos tan تساعدنا بسهولة في احتساب قياس الزاوية بمعرفة أطوال الأضلاع أو معرفة طول الأضلاع بمعرفة الزوايا، حيث أن المقابل والمجاور والوتر هم الأطوال والقوانين الخاصة بحساب ذلك تتضمن كل مما يلي:
- Sin θ أو جيب الزاوية نحتسبه من خلال قسمة الضلع المقابل على الوتر.
- Cos θ أو جيب تمام الزاوية يتم احتسابه بقسمة الضلع المجاور على الوتر.
- Tan θ أو ظل الزاوية يتم احتسابه بقسمة الضلع المقابل على الضلع المجاور.
ومما سبق ذكره نجد أن العلاقة بين الثلاث زوايا تكون عن طريق العلاقة Tan θ = sin θ/cos θ.
المتطابقات المثلثية الأساسية في علم الرياضيات
إن المتطابقات المثلثية أو النسب والاقترانات في المثلث القائم الزاوية في علم الرياضيات قسم حساب المثلثات يتم احتسابها من خلال قوانين معينة والتي تتمثل في كل مما يلي:
- Sine – زاوية الجيب، رمز هذه الزاوية (جا) وقيمة زاويتها من خلال قانون: جا (الزاوية)= الضلع المُقابل للزاوية ÷ وتر المثلث.
- cosine – زاوية جيب التمام، رمزها هو (جتا) والقانون المستخدم لحسابه: جتا (الزاوية)= الضلع المجاور للزاوية ÷ وتر المثلث.
- tangent – زاوية الظل، رمزها هو (ظا) والقانون الذي يحتسب الزاوية هو: ظا (الزاوية)= الضلع المقابل للزاوية ÷ الضلع المجاور للزاوية = جا (الزاوية)/ جتا (الزاوية).
- secant – قاطع الزاوية، رمزها هو (قا)، والقانون الذي يحسب الزاوية هو: قا (الزاوية)= وتر المثلث ÷ الضلع المجاور للزاوية= 1÷ جتا (الزاوية).
- cosecant – قاطع تمام الزاوية، رمزه هو (قتا) وهو مقلوب الجيب ويُحسب من العلاقة: قتا (الزاوية)= وتر المثلث ÷ الضلع المقابل للزاوية = 1÷ جا (الزاوية).
- cotangent – ظل التمام للزاوية، رمزه هو (ظتا)، وهو مقلوب الظا ويُحسب من العلاقة: ظتا (الزاوية)= الضلع المجاور للزاوية÷ الضلع المقابل للزاوية =1÷ ظا س= جتا (الزاوية)/ جا (الزاوية).
قوانين احتساب جيب تمام الزاوية Cos
ج²= أ² + ب² – (2× أ × ب × جتا (جَ)) ، ب² = أ² + ج² – (2 × أ × ج × جتا (بَ)) ، أ² = ج² +ب² -(2 × ب × ج × جتا (أَ)) حيث أن زوايا المثلث هي أ و ب و ج، وكل زاوية تقابل ضلع محدد من المقابل والمجاور والوتر، وإذا كان المثلث قائم الزاوية فإن قيمة جيب التمام يساوي 0 ويتم احتسابه من خلال القانون وفقًا لنظرية فيثاغورث بالعلاقة ج² =أ² +ب².
قوانين احتساب جيب الزاوية Sin
أ/ جا (أَ) = ب / جا (بَ) = ج/ جا (جَ) ، أو جا (أَ) / أ = جا (بَ) / ب = جا (جَ) / ج، ويمكننا توضيح المتغيرات، حيث أن أ، ب، ج هي أضلاع المثلث وكل ضلع يقابله زاوية معينة، وإذا كان المثلث قائم الزاوية فإن قيمة جيب الزاوية يساوي 1.
قوانين احتساب ظل الزاوية Tan
في حالة أنه لدينا مُثلث قائم الزاوية، فإنه إذا كان جيب تمام الزاوية يساوي 0.2 وجيب الزاوية يساوي 0.4 فإنه من خلال قانون ظا أ = جا أ / جتا أ فإن ظا أ = 0>2.
ما هي العلاقة الرياضية بين sin و cos الزاوية؟
تُعد الـ cos مُكملة لـ sin الزاوية المراد احتسابها، وكذلك الـ sin مُكملة لقيمة الـ cos، حيث:
- تُعرف الـ sin بأن لها قيمة يتم احتسابها من خلال النسبة بين طول الضلع المقابل للقائمة إلى الوتر.
- والـ cos تُعرف بأنها قيمة الدالة المثلثية التي تُحسب من النسبة بين طول الضلع المجاور إلى الوتر.
والعلاقة الأساسية بين كل من جيب الزاوية sin وجيب تمام الزاوية cos التي تريد قياسها هي أنه إذا كانت الزاوية المراد قياسها حادة فإن قيمة الـ sin تكون مُكملة للـ cos، ويُعرف بجيب الزاوية التكميلية ويُطرح من 90 الزاوية القائمة، ومثال على ذلك إذا كانت الزاوية 30 فإن مكملتها تكون 60، والمعادلة الحسابية التي تحسب العلاقة هي cos θ = sin (90° – θ).[3].
متى يتم استعمال cos و sin و tan الزاوية؟
بصفة عامة نستخدم قيمة النسب المثلثية للزواية جيب وجيب تمام وظل الزاوية في قياس الزوايا المثلثية ويكون المثلث قائم الزاوية، حيث أنه بمعلومية أطوال أضلاعه فإنه يكون من السهل احتساب الزوايا ودوالها المثلثية، وكل هذه القيم يتم استخدام القيم في حالات معينة وذلك بمعرفة الزاوية واستخدامها في تسمية كل ضلع مما يجاورها أو يُقابلها، حيث:
- عندما تستخدم كل من الوتر والضلع المقابل للزاوية القائمة فإننا هنا نستخدم قانون الجيب sin.
- أما عندما نستخدم كل من الوتر والضلع المجاور للزاوية القائمة فإننا نعتمد قانون جيب التمام cos.
- ولكن إذا استخدمنا كل من الضلع المجاور والمقابل للزاوية القائمة فإننا نستخدم قانون الظل tan.
متطابقات الجمع والضرب في الدوال المثلثية
تشمل هذه المتطابقات بعض العلاقات في الجمع والضرب والتي تتضمن كل مما يلي:
- جا أ جا ب= ½ [جتا (أ – ب) – جتا (س + ص)].
- جتا أ جتا ب= ½ [جتا (أ – ب) + جتا (س + ص)].
- جا أ جتا ب = ½ [جا (أ + ب) + جا (أ – ب)].
- جتا أ جا ب = ½ [جا (أ + ب) – جا (أ – ب)].
متى يساوي جيب تمام الزاوية cos صفرًا؟
يساوي جيب تمام الزاوية صفرًا عندما يتساوى مع طول الضلع المجاور للزاوية القائمة.
حول تعريف الدوال المثلثية بالأعداد المركبة
باستخدام دائرة واحدة يتم تعريف كل من جيب الزاوية وجيب تمامها، ومن خلال علم حساب المثلثات يمكن تعريفها حيث:
- تعتمد هذه الطريقة المتتاليات اللا نهائية باستخدام علم الحساب وتُصاغ بالأعداد المركبة.
- وتتميز الدوال الأسية المركبة بأنه يُستخدم فيها الهندسة والمحركات الكهربائية.
- كما تستخدم حسابات التيار المتردد المستخدمة علم الفلك.
والعلاقة المستخدم في التعريف والتعبير عن هذه العملية هي e x + i y = e x ( cos y + i sin y ) .
تطبيقات على علم المثلثات قوانين sin cos tan
هناك العديد من التطبيقات الحياتية التي نعتمد فيها على علم المثلثات وقوانينه الشهيرة، وتتمثل هذه التطبيقات في كل مما يلي:
- يتم استخدامها في الأجهزة الخاصة بالعرض كالـ Laptops والتلفزيونات وغيرها.
- وتُستخدم أيضًا في إنشاء المباني والأثاث أيضًا.
- كما أنه يستخدم في تخطيط الطرق واحتساب المسافات الجغرافية والفلكية.
- تُصمم وتُخطط بها الملاعب وفقًا لقواعد الألعاب المتنوعة.
- تُحتسب بها المسافات الجغرافية والفلكية البعيدة جدًا.
- الحسابات التي الأنظمة الخاصة بالاستكشاف عبر الأقمار الصناعية.
ولعلنا خلال السطور السابقة في موضوع اليوم تطرقنا إلى أبرز المعلومات عن قوانين sin cos tan للزوايا المثلثية المختلفة وعلاقاتها مع بعضها البعض، كما تعرفنا على أبرز الاستخدامات والتطبيقات الحياتية لها ونتمنى بأنه كان موضوع مفيدًا لكم و لكل طلابنا في مختلف المدارس في المملكة، فعلم الرياضيات هو من أهم العلوم التي ندرسها.